مجموعه ورام
سلام
عید همتون سلو سلو مبارک باشه
با آرزوی هدایت الهی 
و سفر خوشی خرمی براتون آرزومندم فی امان الله
کتابی رو میخوام براتون معرفی کنم بابت عیدی من به شما اگه قابل باشم در زمینه اخلاق که متأسفانه متن کتاب فارسی رو پیدا نکردم به صورت PDF و... ولی در کتابخانه دیجیتال نور میشه خوند و کپی و... متن عربیش هم هست خیلیی راحت میشه دانلود....
برای من که طرفدار کتاب الکترونیکی نیستم بد شد ایضاء نسخه چاپی (ایشلا )
این روزا هم دارم کتاب حق الیقین علامه مجلسی رو میخونم که کتاب در اعتقادات و خیلیی مهم البته سنگین مخصوصا فصل آخر معاد
پیشنهادم اینه دم دست باشه (5 اصول رو اثبات شده داشته باشین)
گذری از دل کتاب :
آداب سیر و سفر، وداع خانواده، و بازگشت از سفر
حسن (١) از رسول خدا (ص) نقل کرده است: «هر کس به خاطر دینش از جایى به جایى بگریزد، هر چند که یک وجب زمین باشد، بهشت بر او واجب شود، و همراه پدرش ابراهیم و پیامبرش محمد (ص) باشد.» (٢) ابو هریره مى‌گوید: پیامبر خدا (ص) فرمود: «اگر مردم رحمت خدا را نسبت به مسافران مى‌دانستند، هر آینه مردم هر بامداد عازم سفر بودند، براستى خداوند نسبت به مسافر، مهربان است.» (٣) هنگامى که حضرت یوسف (ع) از چاه بیرون آورده و خریدارى شد، کسى به ایشان گفت: نسبت به این غریب سفارش خیر و نیکى کنید، یوسف (ع) فرمود: کسى که با خدا باشد غربت براى او معنى ندارد.
امیر المؤمنین (ع) موقع رفتنش به سمت شام عرض کرد: «الهى به تو پناه مى‌برم از رنج سفر و غم بازگشت، و دیدار وضع ناگوار خانواده، مال و فرزند، بار خدایا تو در سفر همراه منى، و در نبودنم سرپرست خانواده‌ام هستى و جز تو کسى نمى‌تواند این دو سمت را داشته باشد، زیرا کسى که جایگزین در خانواده باشد دیگر همراه مسافر نیست، و همراه مسافر نمى‌تواند جانشین در خانواده باشد.» (۴) به ابن اعرابى گفتند: چرا سفر را سفر نامیدند؟ جواب داد: «چون در سفر پرده از اخلاق مردم برداشته مى‌شود.»
دانلود شماره64و65 مجله تهویه و مطبوع
در ادامه دانلود مجله این بار براتون شمارهای 64 و 65 قرار میدم
کمی دیر شد (این چند روز دارم کارگری میکنم )
در ضمن آشنایی دو سایت عالی هم برای شما هدیه
ریکا به سرم می مالیدم!
در پست قبلیم از گوگل مپ استفاده کردم و الان میخوام خاطرهامو باهاش زنده کنم و تقدیم شما و یادگار برای خودم.
البته خاطراتم کوتاه و بعضی شون بلند
به عکس زیر نیگاه کنید این چندسال آلودگی وحشتناک شده که باعث رفتنه اهالی این منطقه شده
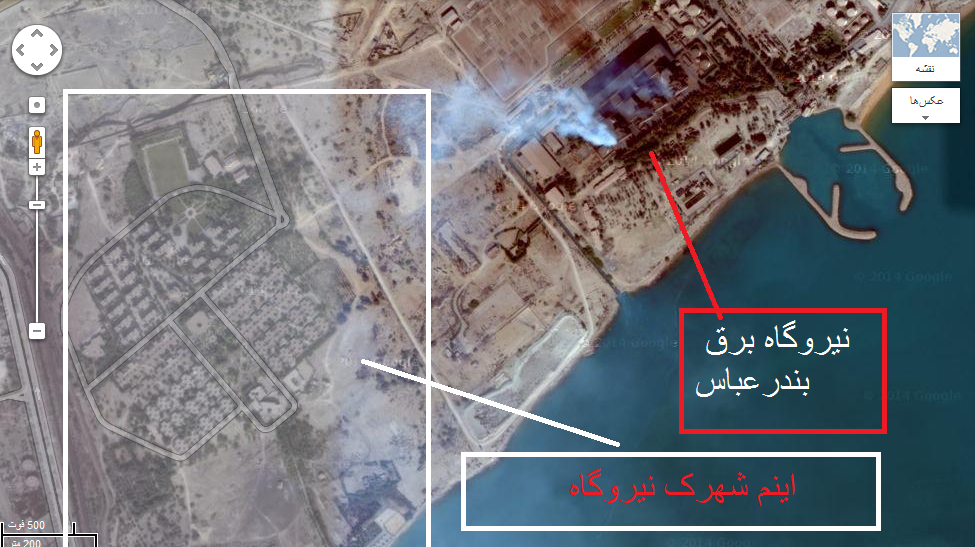
قبل از اینکه بیایم شهر زندگی کنیم من تا سن 13 سالگی در شهرک توانیر زندگی میکردم که واسم حکم بهشت داره با تمامی امکانات رفاهی (سالن های ورزشی بزرگ ، زمین فوتبال چمنی،آسفالت،سالنی،استخرو... و مکانهای تفریحی و پول آب و برق و گاز و تلفن رایگان بگیر تا .... خدایش تو بهشت زندگی میکردیم ولی الان اونجا پولی شده وقتی ما اومدیم بیرون
خاطره 1.
یادمه اون موقع ها من و چندی از دوستانم پولامون رو روی هم میزاشتیم بعدش میرفتیم کتیرا واسه خودمون میخریدم و
میزدیم به سرمون و کلی ذوق و شوق . بعدش وقتی میخواستیم بریم خونه هامون دیگه میترسیدیم که بابا و مادرامون کتکمون بزنن چون اون موقع ها نمیزاشتن ما به سرمون چیزی بزنیم ، حالا مونده بودیم شیشه کتیرا رو دست کی بدیم و هم فکری کردیم و رفتیم پشت خونه ما (عکسو نیگاه کنید) بعد زیر یکی از درخت ها گودالی کندیم و گذاشتیم اونجا فرداش دیگه میرفتیم بقیشو استفاده میکردیم این مخفی کردن اولین بارمون نبود یادمه واسه کادو روز مادرم رفتم یه اسپره خوشبوکننده خریدم و واسه اینکه نبرم خونه رفتم زیر همین درختا مخفیش کردم ، بعضی موقع ها هم که پول کتیرا و نداشتیم من میرفتم دوزدکی تو آشپزخونه یکمی ریکا رو می ریختم روی سرم و نرم میشد و جلوی دوستانم کلاس میزاشتم و بهشون میگوفتم دست بزن عجب نرم شده!محسن 
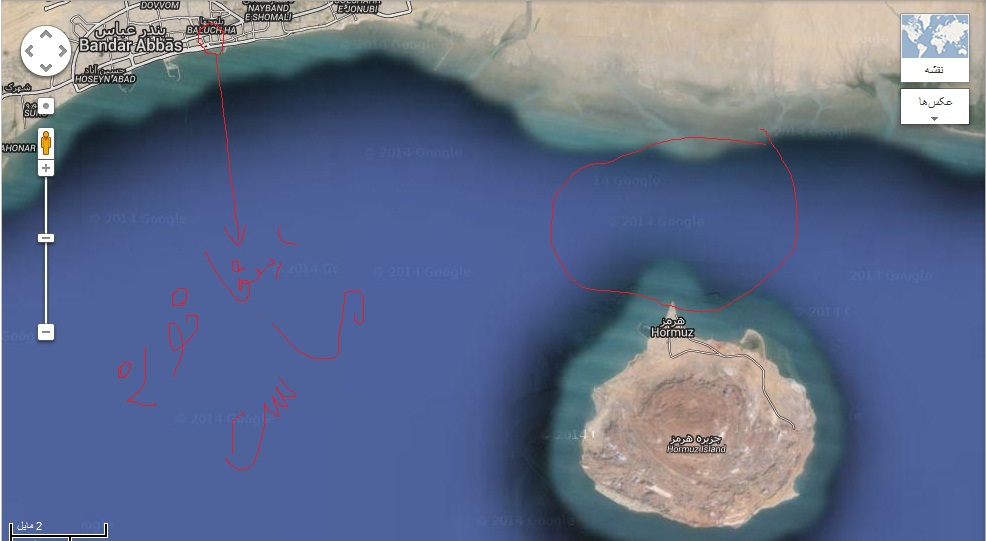
طرحی از ساخت نیروگاه تالابی
فاصله بین بندرعباس و جزیره همه رنگ هرمز همچنین اتفاقی رخ میده و سرعت جریان آب در جزر و مد زیاد میشه و مناسب واسه همچین طراحی هست. و جالبه عمق آب هم کم هستش و الان اونجا هم دارند یه پلان تفریحی میسازن خیلیی بزرگ که با این ساخت نیروگاه میتونند برق خودشو تأمین کنه ! کنارشم بزرگ ترین آب شیرکن خاورمیانه (گمونم) درست دارند میکنند (زمان احمدی نژاد به احتمال) که آب رو از اینجا واسه هم استانی های مجاور مخصوصا یزد پمپاژ کنند. واسه ما هم اشتغالزایی میشه.
عکساش هم، زیر قرار دادم حتما ببینید.
یاد آوری آموزش قرآن
همه تو دوران بچگیشون مخصوصا تابستونا میرفتن کلاس قرآن عحب دورانی بود یادش بخیر خوب اون بچگی بود و تا الان که بزرگ شدیم و یه مهندسی زیر بغلمون هستش و بعضی هم دکترا
، بعضی از تجوید ها رو یادشون باید بره اونای که از همون بچه گی پیگیر بودن و مرور میکردن که حسابشون جدا ولی بعضی از ماها یکی مثل خودم بعد چند سال خیلیی چیزا رو فراموش کردیم و غلط تجویدی تا دلت بخواد داریم . 
تو این چند سال خیلیی پیگیر بودم که بشینم دوباره قرآن رو یادبگیرم و موفق شدم یه مدت کوتاهی برم کلاس که بعدش خورد به رمضان و تعطیل و بعدش کنکور ،کنکور تا الان (حتی بعضی موقع ها فکر میکنم اگه این همه زمان رو واسه کنکور خرج نمیکردم و بجاش قرآنمو درست میکردم الان خیلیی وقت بود فول بودم ها
) خوب هنوز دیر نیست چندماه فرصت دارم که برم کلاس و دوباره استارت بزنم از دیروز هم مرور کردم و از امشب هم به مدت 10 دقیقه میرم کلاس ایشلا.
پیغام به دوستان وبلاگی مون هم اینه که سعی کنن اگه تا هنوز سراغ قرآن نرفتن و فراموشی سراغشون اومده یه چند واحد کلاس قرآن رفتن و پاس کردن ضرری نداره در وقت و پولتون بلکه ............هم داره ! (جاخالی رو خودتون پر کنید )
بارها شندیم از اینور اونور که حق پدر و مادر به فرزندان خود، یکیش اینه قرآن بیاموزند، نمیخوام فردای قیامت جلو پدرومو بگیرن که چرا ............
خوب اونچیزی که لازم بود رو بهتون یادآوری کردم در پایین میخوام یادآوردی کنم بعضی از تجوید های قرآنی که خیلیی ساده و با یه مرور تلاوتون خیلیی عالی میشه.
بسم الله الرحمن الرحیم
علامت قرآن 11 است:
اَ فتحه
اِ کسره
اُ ضمّه
این سه حرکت بالا را صدای کوتاه می نامند
اً تنوین ، نصب
اٍ تنوین ، جر
اُُ تنوین ، رفع
تعریف تنوین : همان (ن) ساکن است که نوشته نمی شود ولی خوانده می شود:
مثال :
ربّاََ : رَبَّنْ کتابِِ : کتابنْ
__ّ تشدید (توفارسی هستش)
______ْ ساکن : باز ایستادن از حرکت توقف بر حروف مثال : رَهَیْتُ
پست ناقص ایشلا بعد کامل میشه
استاندارد پمپ ها
در این پست نمیخوام این پمپ رو تعریف کنم دیگه چیز تکراری شده، میخوام شما را با استاندارد های بکار رفته پمپ در صنعت آشنا کنم .
در صنعت 80 درصد از پمپ های صنعتی،پمپ های گریز از مرکز، تک مرحله ای و تک وردی هستند.در میان کلیه این پمپ ها دو نوع پمپ از همه متداول تر است که عبارت میشه :
1.ANSI که بر طبق استاندادر موسسه استاندارسازی آمریکا
2.API که برطبق استاندارد 610 موسسه نفت آمریکا جهت خدمات پالایشگاه طراحی و ساخته شده اند
با توجه اینکه هر کشوری معیار و خاص خود را دارد، بطور مثال :
1.استاندارد بین الملی ISO،
2. DIN آلمان
3.BC انگلیس
که به طور کلی ساختار پمپ ها شباهت زیادی به API , ANSI دارند.
کابرد پمپ ANSI برای فرآیند های شیمیای،آب و سایر مایعات با خاصیت خورندگی کمتر و برای پمپ API به تصیفه نفت و صنایع مربوطه بهترین انتخاب ها می باشد.
تفاوت عمده بین این دو مدل،در درجه بندی طرح فشار پوسته و به شرح ذیل است:
درجه بندی پمپ ANSI=300PSIG در دمای 300 درجه فارنهایت
درجه بندی پمپ API =750PSIG در دمای 500 درجه فارنهایت
این اعداد نشان گر پمپ API را می توان برای کار با فشار و دمای بالا مورد استفاده قرار داد در حالی که پمپ ANSI برای عملیات های سبک تر مفید و کار آمد محسوب می شود.
خوب تا اینجا بسه ادامه متن رو با شکل های مرتبط در لینک زیر دریافت کنید
کک سازی !
چنتا لینک قرار میدم در باره کک سازی از زغال سنگ ، فیلم شو دیدم جالب بود .
برای من که فولاد هرمزگان و خلاصه قطب صنعت بغل خونمون است آشنایی به این موارد ضروت داره ! واسه همین چنین مطالبی ازم خواهید دید...
برای آشنایی بیشتر سرچ کنید ایشلا مفید باشه!